|
Subject
Customer
Location
Job No.
Engr.
Rev.
Date
Page
This report may not be copied, reproduced or distributed without the written consent of
Medeek Engineering Inc.
Copyright © 2014
Beam Design
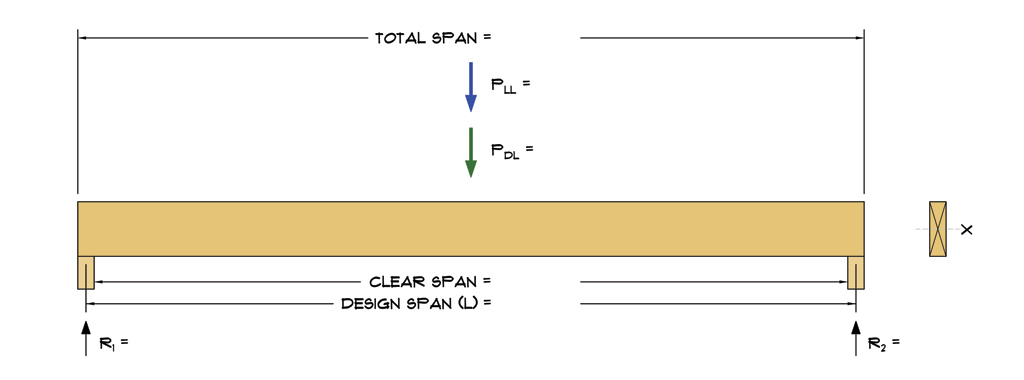
1. Beam Data
| Load Type: | Single Point Load | |
| Support: | Simple Beam | |
| Beam Type: | Sawn Lumber | |
| Species: | Western Cedars | |
| Grade: | WC No.2 | |
| Size: | 4 x 12 | |
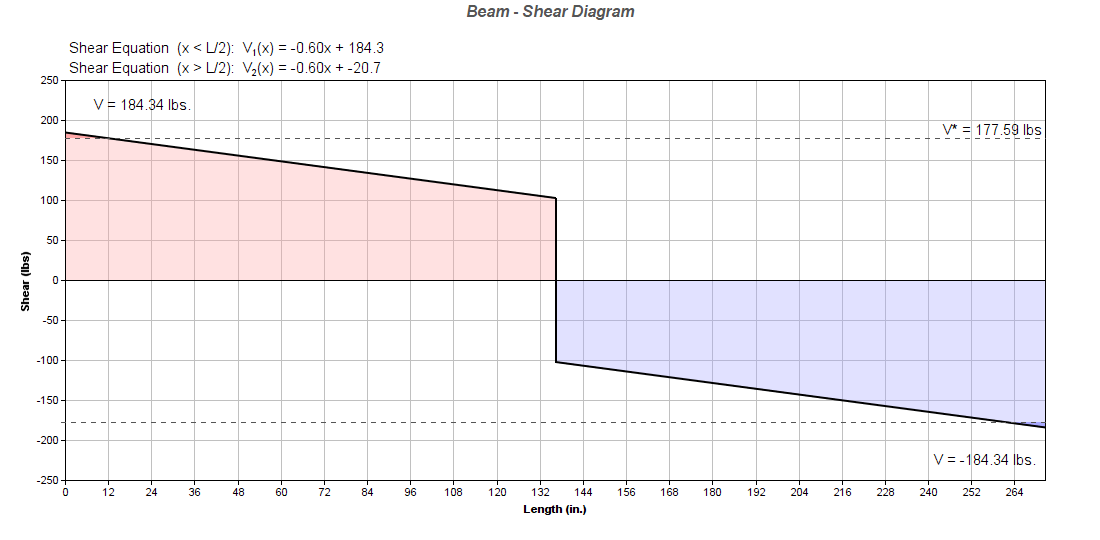
| Design Span (L): | 22.71 | ft. |
| Clear Span: | 22.42 | ft. |
| Total Span: | 23.00 | ft. |
| Bearing (lb): | 3.5 | in. |
| Quantity (N): | 1 | |
|
2. Design Loads
| Live Load: | 180 | lbs |
| Dead Load: | 25 | lbs |
| Selfweight: | 163.7 | lbs |
| Dist. Selfweight: | 7.21 | plf |
| Total Weight: | 165.8 | lbs |
|
3. Design Options
| Lateral Support: | unbraced |
| Defl. Limits: | 240|180 |
| Load Duration: | 1.00 |
| Exposure: | wet |
| Temperature: | 100°F < T <= 125°F |
| Orientation: | Vertical |
| Incised Lumber: | No |
| Rep. Members: | No |
|
4. Design Assumptions and Notes
| Code Standard: | IBC 2015, NDS 2015 |
| Bending Stress: | Parallel to Grain |
| Notes: | |
|
5. Adjustment Factors
| Factor | Description | Fb | Ft | Fv | Fc | Fc⊥ | E/Emin |
| CD | Load Duration Factor | 1.00 | 1.00 | 1.00 | 1.00 | - | - |
| CM | Wet Service Factor | 1b | 1 | 0.97 | 1c | 0.67 | 0.9 |
| Ct | Temperature Factor | 0.7 | 0.9 | 0.7 | 0.7 | 0.7 | 0.9 |
| CL | Beam Stability Factor | 0.947 | - | - | - | - | - |
| CF | Size Factor | 1.1 | 1 | - | 1 | - | - |
| Cfu | Flat Use Factor | 1.1d | - | - | - | - | - |
| Ci | Incising Factor | 1 | 1 | 1 | 1 | 1 | 1 |
| Cr | Repetitive Member Factor | 1 | - | - | - | - | - |
a) Adjustment factors per AWC NDS 2015 and NDS 2015 Supplement.
b) When (Fb)(CF) ≤ 1,150 psi, CM = 1.0.
c) When (Fc)(CF) ≤ 750 psi, CM = 1.0.
d) Only applies when sawn lumber or glulam beams are loaded in bending about the y-y axis.
|
|