Subject

Customer

Location

Job No.

Engr.

Rev.

Date

Page

This report may not be copied, reproduced or distributed without the written consent of
Medeek Engineering Inc.

Copyright © 2014

Beam Design

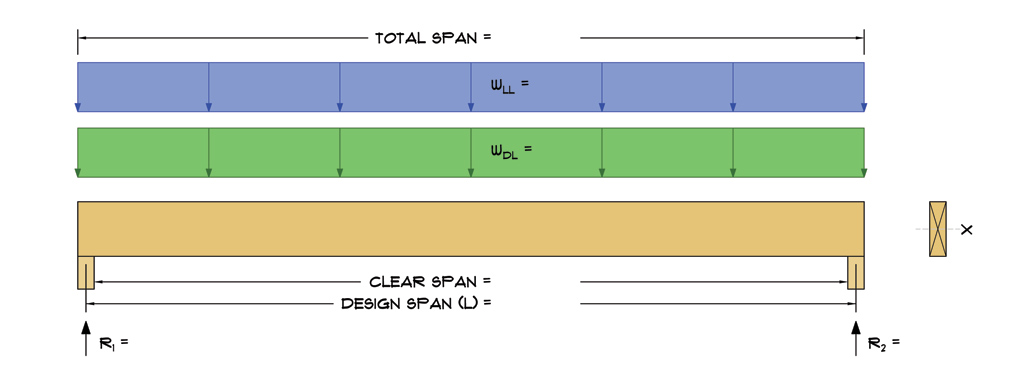
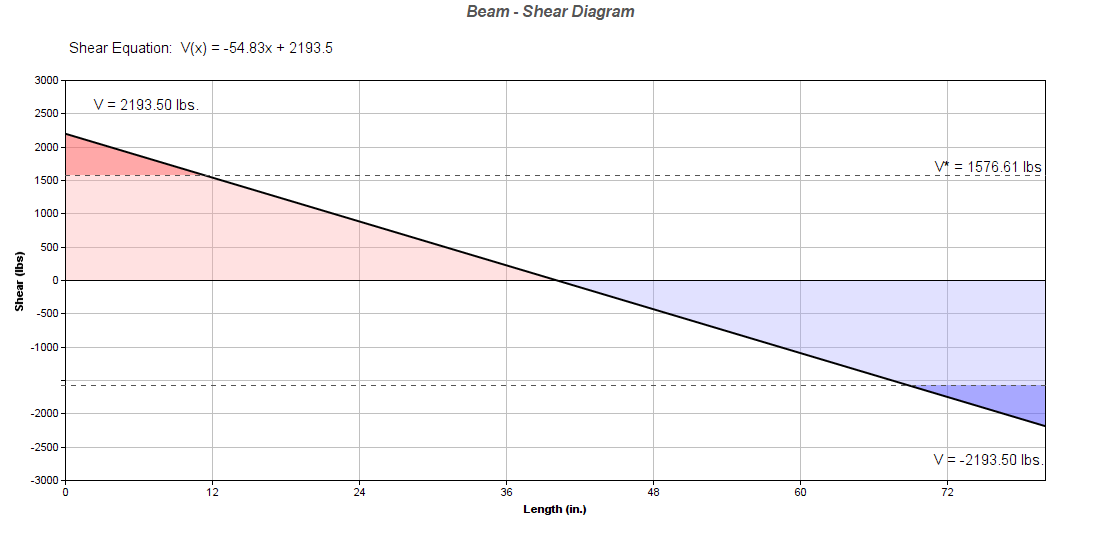
1. Beam Data

Load Type:	Uniform Dist. Load
Support:	Simple Beam
Beam Type:	Sawn Lumber
Species:	Douglas Fir-Larch
Grade:	DF No.2
Size:	2 x 12
Design Span (L):	6.67	ft.
Clear Span:	6.42	ft.
Total Span:	6.92	ft.
Bearing (l_b):	3	in.
Quantity (N):	2

2. Design Loads

Live Load:	500	plf
Dead Load:	150	plf
Selfweight:	53.4	lbs
Dist. Selfweight:	8.02	plf
Total Weight:	55.4	lbs

3. Design Options

Lateral Support:	unbraced
Defl. Limits:	240\|180
Load Duration:	1.00
Exposure:	dry
Temperature:	T <= 100°F
Orientation:	Vertical
Incised Lumber:	No
Rep. Members:	No

4. Design Assumptions and Notes

Code Standard:	IBC 2015, NDS 2015
Bending Stress:	Parallel to Grain
Notes:

5. Adjustment Factors

Factor	Description	F_b	F_t	F_v	F_c	F_c⊥	E/E_min
C_D	Load Duration Factor	1.00	1.00	1.00	1.00	-	-
C_M	Wet Service Factor	1^b	1	1	1^c	1	1
C_t	Temperature Factor	1	1	1	1	1	1
C_L	Beam Stability Factor	0.983	-	-	-	-	-
C_F	Size Factor	1	1	-	1	-	-
C_fu	Flat Use Factor	1.2^d	-	-	-	-	-
C_i	Incising Factor	1	1	1	1	1	1
C_r	Repetitive Member Factor	1	-	-	-	-	-

                  a) Adjustment factors per AWC NDS 2015 and NDS 2015 Supplement.
                  b) When (F_b)(C_F) ≤ 1,150 psi, C_M = 1.0.
                  c) When (F_c)(C_F) ≤ 750 psi, C_M = 1.0.
                  d) Only applies when sawn lumber or glulam beams are loaded in bending about the y-y axis.

Beam Design

2020A275

N. Wilkerson

MEDEEK ENGINEERING INC.
3050 State Route 109 Copalis Beach, WA 98535
ph. (425) 741-5555 www.medeek.com

12/8/2020

Subject

Customer

Location

Job No.

Engr.

Rev.

Date

Page

This report may not be copied, reproduced or distributed without the written consent of
Medeek Engineering Inc.

Copyright © 2014

6. Beam Calculations

Determine reference design values, sectional properties and self weight of beam:

A = b x d

$S_{x}=\frac{bd^2}{6}$ , $S_{y}=\frac{b^{2}d}{6}$

$I_{x}=\frac{bd^3}{12}$ , $I_{y}=\frac{b^{3}d}{12}$

where:

b = Breadth of rectangular beam in bending (in.)
d = Depth of rectangular beam in bending (in.)
A = Cross sectional area of beam (in.²)
S_x = Section modulus about the X-X axis (in.³)
S_y = Section modulus about the Y-Y axis (in.³)
I_x = Moment of inertia about the X-X axis (in.⁴)
I_y = Moment of inertia about the Y-Y axis (in.⁴)

b = 1.500 in.
d = 11.250 in.
A = 1.500 x 11.250 = 16.88 in.²
S_x = (1.500)(11.250)²/6 = 31.64 in.³
S_y = (1.500)²(11.250)/6 = 4.22 in.³
I_x = (1.500)(11.250)³/12 = 177.98 in.⁴
I_y = (1.500)³(11.250)/12 = 3.16 in.⁴

Reference Design Values from Table 4A NDS Supplement (Reference Design Values for Visually Graded Dimension Lumber, 2" - 4" thick).

Species & Grade	F_b	F_t	F_v	F_c⊥	F_c	E	E_min	G
DF No.2	900	575	180	625	1350	1600000	580000	0.5

The following formula shall be used to determine the density of wood (lbs/ft³. (NDS Supplement Sec. 3.1.3)

$\rho_{w}=62.4\left[\frac{G}{1+G(0.009)(m.c)}\right]\left[1+\frac{m.c.}{100}\right]$

where:

ρ_w = Density of wood (lbs/ft³
G = Specific gravity of wood (dimensionless)
m.c. = Moisture content of wood (percentile)

G = 0.5
m.c. = 19 % (Max. moisture content at dry service conditions)

Beam Design

2020A275

N. Wilkerson

MEDEEK ENGINEERING INC.
3050 State Route 109 Copalis Beach, WA 98535
ph. (425) 741-5555 www.medeek.com

12/8/2020

Subject

Customer

Location

Job No.

Engr.

Rev.

Date

Page

This report may not be copied, reproduced or distributed without the written consent of
Medeek Engineering Inc.

Copyright © 2014

$\rho_{w}=62.4\left[\frac{0.5}{1+0.5(0.009)(19)}\right]\left[1+\frac{19}{100}\right]$ = 34.20 lbs/ft³

Volume_total = N[A x (L + l_b)] = 2 x [16.88 x (80.00 + 3)] x (12 in./ft.)³ = 1.62 ft³
Volume_span = N[A x L] = 2 x [16.88 x 80.00] x (12 in./ft.)³ = 1.56 ft³

Total Weight (W_T) = ρ_w x Volume_total = 34.20 x 1.62 = 55.4 lbs
Self Weight (W_S) = ρ_w x Volume_span = 34.20 x 1.56 = 53.4 lbs

Distributed Self Weight (w_s) = $\frac{W_{S}}{L}=\frac{53.4}{6.67}$ = 8.02 plf

Load, Shear and Moment Diagrams:

500 plf

150 plf

w_s = 8.02 plf

6.67 ft.

6.42 ft.

6.92 ft.

2275.75 lbs

Beam Design

2020A275

N. Wilkerson

MEDEEK ENGINEERING INC.
3050 State Route 109 Copalis Beach, WA 98535
ph. (425) 741-5555 www.medeek.com

12/8/2020

Subject

Customer

Location

Job No.

Engr.

Rev.

Date

Page

This report may not be copied, reproduced or distributed without the written consent of
Medeek Engineering Inc.

Copyright © 2014

1.) Bending:

Members subject to bending stresses shall be proportioned so that the actual bending stress or moment shall not exceed the adjusted bending design value:

f_b ≤ F_b' (NDS Sec. 3.3.1)

where:

f_b = M / S
F_b' = F_b(C_D)(C_M)(C_t)(C_L)(C_F)(C_i)(C_r)

Beam is unbraced along its compression edge, lateral stability is considered below:

Slenderness Ratio for bending member R_B:

l_u = Unbraced Length = 6.667 ft.

l_u/d = $\frac{80.004}{11.25}$ = 7.11

l_e = 1.63l_u + 3d = 1.63(80.0) + 3(11.25) = 164.16 in. = 13.68 ft. (NDS Table 3.3.3)

R_b = $\sqrt{\frac{l_{e}d}{b^2}}=\sqrt{\frac{164.16(11.25)}{(2\times1.5)^{2}}}$ = 14.32

R_b = 14.32 < 50 ➜ OK

Beam Design

2020A275

N. Wilkerson

MEDEEK ENGINEERING INC.
3050 State Route 109 Copalis Beach, WA 98535
ph. (425) 741-5555 www.medeek.com

12/8/2020

Subject

Customer

Location

Job No.

Engr.

Rev.

Date

Page

Euler-based ASD critical buckling value for bending members:

E_miny' = E_miny(C_M)(C_t)(C_i) = 580000(1)(1)(1) = 580000 psi

F_bE = $\frac{1.2E_{miny}'}{(R_{b})^2}=\frac{1.2(580000)}{(14.32)^2}$ = 3391.88 psi

F_bx* = F_bx(C_D)(C_M)(C_t)(C_F)(C_i)(C_r) = (900)(1.00)(1)(1)(1)(1)(1) = 900.00 psi

Beam stability factor:

C_L = $\frac{1+F_{be}/F_{bx}^*}{1.9}-\sqrt{\left(\frac{1+F_{be}/F_{bx}^*}{1.9}\right)^2-\frac{F_{be}/F_{bx}^*}{0.95}}=$ $\frac{1+3391.88/900.00}{1.9}-\sqrt{\left(\frac{1+3391.88/900.00}{1.9}\right)^2-\frac{3391.88/900.00}{0.95}}$ = 0.983

F_bx' = (900)(1.00)(1)(1)(0.983)(1)(1)(1) = 884.4 psi

f_b = $\frac{M}{N\times{S_{x}}}=\frac{43872}{2\times31.64}$ = 693.3 psi

f_b = 693.3 psi < F_bx' = 884.4 psi (CSI = 0.78)   ➜  OK

2.) Shear:

Members subject to shear stresses shall be proportioned so that the actual shear stress parallel to grain or shear force at any cross section of the bending member shall not exceed the adjusted shear design value:

f_v ≤ F_v' (NDS Sec. 3.4.1)

where:

f_v = $\frac{3V}{2A}$

F_v' = F_v(C_D)(C_M)(C_t)(C_i)

F_vx' = (180)(1.00)(1)(1)(1) = 180.00 psi

Shear Reduction: Uniformly distributed loads within a distance, d, from supports equal to the depth of the bending member shall be pemitted to be ignored. Concentrated loads within a distance equal to the depth of the bending member from supports shall be permitted to be multiplied by x/d where x is the distance from the beam support face to the load. See NDS 2015, Figure 3C.

f_v* = $\frac{3V^*}{2(N\times{A})}=\frac{3(1576.61)}{2(2\times16.88)}$ = 70.07 psi

f_v* = 70.07 psi < F_vx' = 180.00 psi (CSI = 0.39)   ➜  OK

No Reduction in Shear (conservative):

f_v = $\frac{3V}{2(N\times{A})}=\frac{3(2193.50)}{2(2\times16.88)}$ = 97.49 psi

f_v = 97.49 psi < F_vx' = 180.00 psi (CSI = 0.54)   ➜  OK

Beam Design

2020A275

N. Wilkerson

MEDEEK ENGINEERING INC.
3050 State Route 109 Copalis Beach, WA 98535
ph. (425) 741-5555 www.medeek.com

12/8/2020

Subject

Customer

Location

Job No.

Engr.

Rev.

Date

Page

3.) Deflection:

Bending deflections calculated per standard method of engineering mechanics for live load and total load:

LL Allowable: L/240
TL Allowable: L/180

E_x' = E_x(C_M)(C_t)(C_i) = 1600000(1)(1)(1) = 1600000 psi

Δ_LL = $\frac{5w_{LL}L^4}{384E_{x}'(N\times{I_{x}})}=\frac{5(500)(6.667)^4}{384(1600000)(2\times177.98)}\times\left(12\frac{in.}{ft.}\right)^3$ = 0.04 in.

(L/d)_LL = 80.00 / 0.04 = 2050

Δ_LL = 0.04 in = L/2050 < L/240   ➜  OK

Δ_TL = $\frac{5(w_{TL}+w_{s})L^4}{384E_{x}'(N\times{I_{x}})}=\frac{5(650+8.02)(6.667)^4}{384(1600000)(2\times177.98)}\times\left(12\frac{in.}{ft.}\right)^3$ = 0.05 in.

(L/d)_TL = 80.00 / 0.05 = 1558

Δ_TL = 0.05 in = L/1558 < L/180   ➜  OK

4.) Bearing:

Members subject to bearing stresses perpendicular to the grain shall be proportioned so that the actual compressive stress perpendicular to grain shall be based on the net bearing area and shall not exceed the adjusted compression design value perpendicular to grain:

f_c⊥ ≤ F_c⊥' (NDS Sec. 3.10.2)

where:

f_c⊥ = $\frac{R}{A_b}$

F_c⊥' = F_c⊥(C_M)(C_t)(C_i)

F_c⊥x' = (625)(1)(1)(1) = 625.00 psi

A_b = b x l_b = 1.5 x 3 = 4.50 in²

f_c⊥ = $\frac{R}{N\times{A_{b}}}=\frac{2275.75}{2\times4.50}$ = 252.9 psi

f_c⊥ = 252.9 psi < F_c⊥x' = 625.00 psi (CSI = 0.40)   ➜  OK

*Disclaimer: The calculations produced herein are for initial design and estimating purposes only. The calculations and drawings presented do not constitute a fully engineered design. All of the potential load cases required to fully design an actual structure may not be provided by this calculator. For the design of an actual structure, a registered and licensed professional should be consulted as per IRC 2012 Sec. R802.10.2 and designed according to the minimum requirements of ASCE 7-10. The beam calculations provided by this online tool are for educational and illustrative purposes only. Medeek Design assumes no liability or loss for any designs presented and does not guarantee fitness for use.

Beam Design

2020A275

N. Wilkerson

MEDEEK ENGINEERING INC.
3050 State Route 109 Copalis Beach, WA 98535
ph. (425) 741-5555 www.medeek.com

12/8/2020